応用数学勉強会2013 @芝浦工大
期間 2013年12月16日(月)~12月17日(火)
会場 芝浦工業大学大宮キャンパス
5号館数理棟2F ゼミ室2
会場へのアクセス: http://www.shibaura-it.ac.jp/access/index.html
キャンパス内の順路は下記参照。
講師
大塚 岳 氏(群馬大学)
降旗 大介 氏(大阪大学)
レクチャーノート公開(2014.9.12 随時更新します)
大塚氏レクチャーノート
降旗氏レクチャーノート
プログラム
【12月16日(月)】
講義A: 大塚 岳 氏 「界面の発展現象に対する等高面の方法」
13:00~14:15 1コマ目
14:30~15:45 2コマ目
16:00~17:15 3コマ目
【12月17日(火)】
講義B: 降旗 大介 氏 「構造保存数値解法入門 -離散変分導関数法-」
10:00~11:15 1コマ目
11:30~12:45 2コマ目
13:45~15:00 3コマ目
各講義の内容
講義A 「界面の発展現象に対する等高面の方法」
講師: 大塚 岳 氏(群馬大学)
アブストラクト
界面や曲面の運動を表すもっとも素朴な方法は界面の位置を通常の
パラメータと時間のパラメータによりパラメータ表示して、各点の
動きを表す微分方程式を解くことである。
例えば曲線短縮方程式として知られる曲率流方程式はパラメータ表
示された曲線における各成分の熱方程式として表されることが知ら
れている。ところがパラメータ表示による界面運動の表示は、例え
ば2カ所から界面の成長が始まっていずれ界面同士が接触するよう
な、特異点を持つ状況では破綻する。
この特異点を含む界面の発展現象を記述する方法として、等高面法
はとても有力な手法である。等高面法とは界面を補助曲面のゼロ等
高面として表す方法で、曲線や曲面が特異点を含むような運動も滑
らかな関数の滑らかな運動として表しうる可能性を持つ。
他方で、例えば前述の曲率流方程式は等高面法で表すと非発散型で
退化放物型の微分方程式となり、いわゆる超関数の意味での弱解理
論の適用が難しい。さらに等高面法特有の問題として、一つの界面
に対しこれをゼロ等高面として表す補助関数は一意ではないという
問題があり、等高面法による界面運動の一意性は界面の運動を表す
微分方程式の解の一意性とは別に改めて考える必要がある。
そこで、本講演ではまず界面の幾何学的発展方程式である平均曲率
流方程式を中心に、等高面法による定式化の方法について解説する。
次に、等高面法から得られる発展方程式の解の一意性および存在を、
退化放物型方程式に対する粘性解理論をもとに紹介する。最後に、
解の一意性の証明で用いる比較原理の応用として等高面法による界
面運動の一意性について証明する。
講義B 「構造保存数値解法入門 -離散変分導関数法-」
講師: 降旗 大介 氏(大阪大学)
アブストラクト
数値解析において,微分方程式の数値解法は理論上も実用上も重要なもの
である.そのため半世紀以上にわたって多くの研究が積み重ねられ,速度,
精度,安定性などの視点に基づいて解法の改良が進められてきている.
そうした視点の1つとして解のなんらかの性質を数値的に(なるべく良く)再
現することを「構造保存性」と呼んでこれに着目する考え方があり,近年
注目されてきている.
こうした解法として,常微分方程式で記述されるハミルトン系に対するシ
ンプレクティック性を保存するシンプレクティック解法でがよく知られて
いるが,近年は偏微分方程式系に対しても系の第一積分を保存ないしは散
逸する解法なども開発,研究されるようになってきている.
本機会においては,こうした解法の考え方や理論の展開について解説し,
時間が許せば偏微分方程式に対する一方法である離散変分導関数法につい
ても紹介する.
※懇親会のお知らせ
勉強会初日(12月16日)に懇親会を東大宮あるいは大宮周辺で予定しています。
懇親会に参加される方は、12月8日までに石渡までご連絡ください。
大宮キャンパス内順路
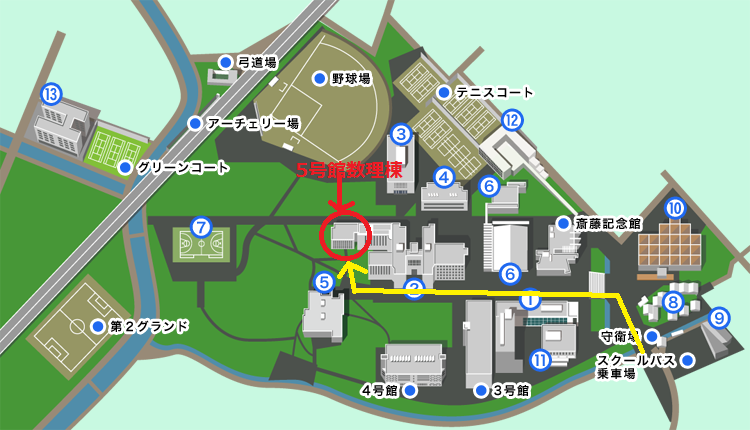
① 2号館(講義棟)
② 5号館
⑤ 図書館
⑥ 体育館
⑩ 生協
連絡先
石渡 哲哉(芝浦工業大学)tisiwata(at)shibaura-it.ac.jp
高坂 良史(室蘭工業大学)kohsaka(at)mmm.muroran-it.ac.jp
更新日 2013年11月13日
